With the sheer number of cryptocurrencies that exist (2.4 million listed tokens as of 2024), there has to be a way to convert value from one currency to the next. When the idea of changing one currency into another arises in our mind, we intuitively think of a money changer, a concept that is familiar to fiat currency.

However, many characteristics of a money changer, such as its centralized nature, are incongruent with DeFi. So how might we solve the problem of token swapping?

DeFi came up with a solution in the form of Automated Market Makers

What is an Automated Market Maker?

An Automated Market Maker (AMM) is a type of decentralized exchange that uses smart contracts and algorithms to facilitate trading of different cryptocurrencies (usually two; Bitcoin to Ethereum let’s say) without the need for an intermediary. Think of this as a automated money changer, ran by code instead of people.

Like its name suggests, each AMM can create markets for each token pair, which are called liquidity pools. It’s important to note each liquidity pool holds its own stash of tokens, rather it than it being stored centrally in the AMM.

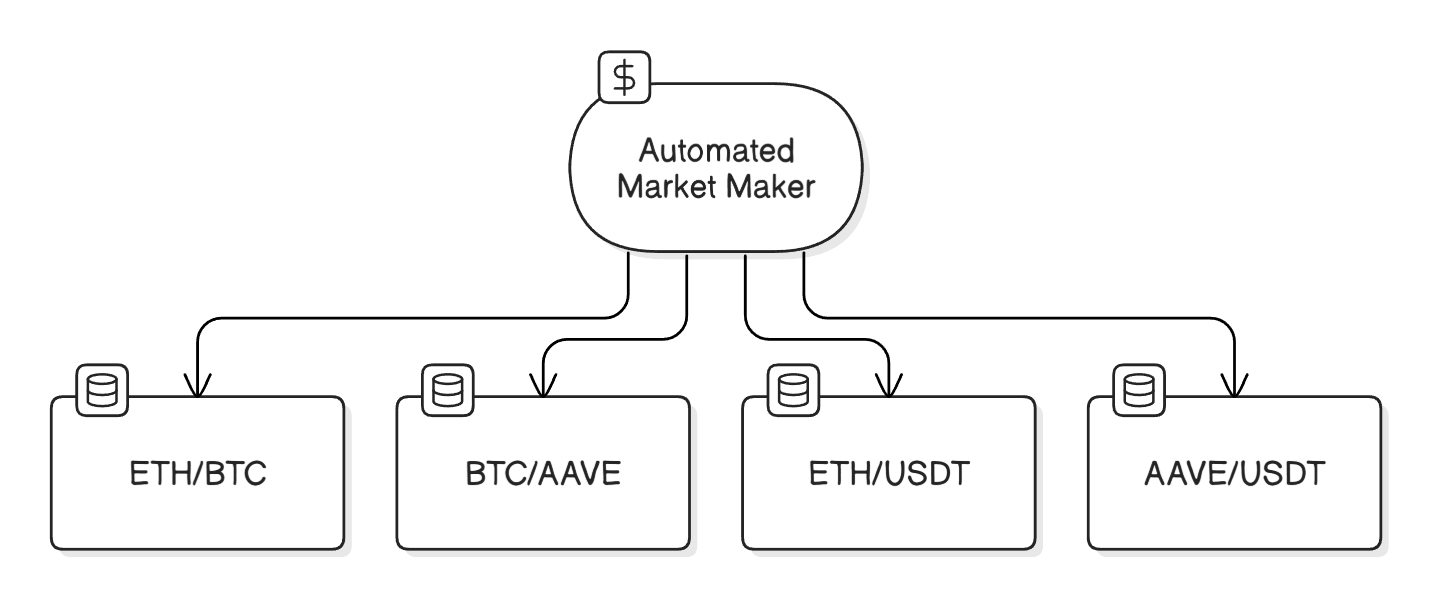An AMM can create multiple liquidity pools to facilitate trading between different tokens

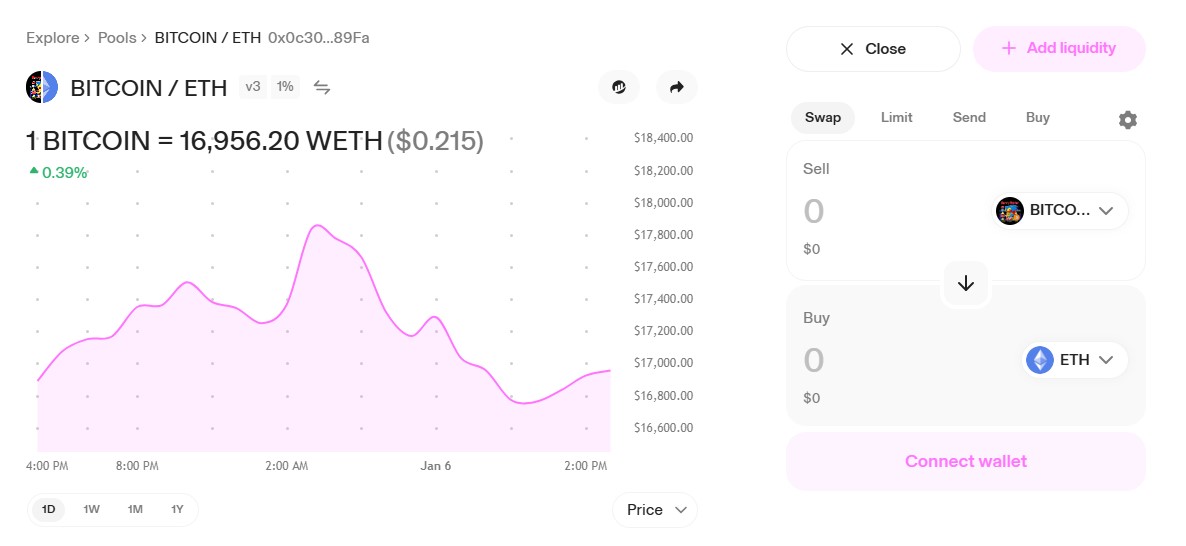A liquidity pool created by an Automated Market Maker, providing a token swap from Bitcoin and Ethereum

Well, then where do the tokens come from? The smart contract can’t give you Ethereum for your Bitcoin if it only have Bitcoin in it’s pool of tokens. Any working exchange needs a sizable amount of both tokens to facilitate exchange.

The tokens that are held by this contract is referred to as liquidity.

The people who provide this liquidity to the pool, are referred to as liquidity providers

The people who use the tool to change tokens, we will refer to as traders

1. Pricing

So, a quick recap, Automated Money Makers use smart contracts to create liquidity pools, which in turn hold liquidity (tokens) provided by Liquidity Providers. Traders who want to exchange token can then access the liquidity pool. But how do we establish the price (exchange rate) of the tokens? How do we know, for example, how much Bitcoin should the pool offer when a user wants to swap a sum of Ethereum into Bitcoin?

1.1 Price Setting

Where do we this price? The price is originally set by the liquidity providers who deposit tokens into the pool!

When depositing tokens, liquidity providers deposit an equal value of each token in the pool (not to be confused with equal quantity). Let’s say Bitcoin is 10 times the value of Ethereum, then liquidity providers will have to deposit in a ratio of 10 ETH to 1 BTC.

1.2 Price Curve (Constant Sum)

Now we that we know the price, we can model the state of the liquidity pool at any given time with the mathematical expression:

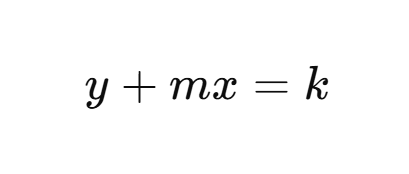Constant Sum Equation

This is the most simplistic way a smart contract can model currency in a liquidity pool (we’ll be covering more later one) where:

1. Gradient m represents the exchange rate (price of tokens in relation to one another)
2. Constant k represents the overall value of tokens in the pool
3. Coordinates X and Y represent the number of tokens in the pool at a point on the curve

Let’s look at it in graphical format here:

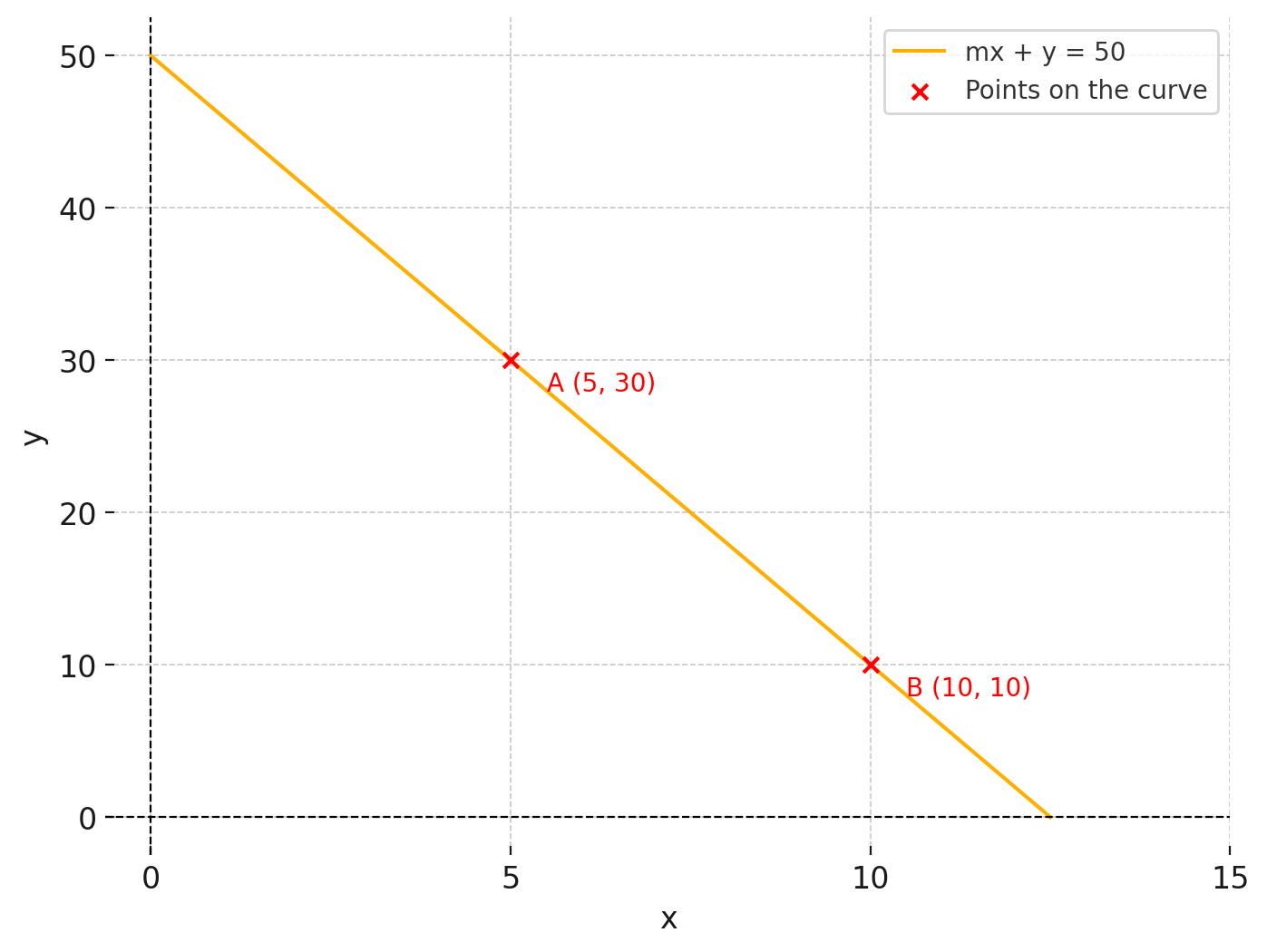Constant Sum Graph

In this curve, the liquidity pool is represented with the equation y + 4m = 50, with the m gradient value of 4 and the k total token value of 50.

In the above graph we have two coordinates (5,30 and 10,10) that represent different state of the pools, where user’s interaction with the pool changes the coordinates along the line of the curve, changing the number of each token in the pool.

Hence, movement from point A to point B on the curve represents the addition of 5 tokens of X and the removal of 20 tokens of Y, as 4 tokens of Y is equivalent to 1 token of X.

1.2.1 Issue with Constant Sum

Constant sum seems like an easy and straight forward way to liquidity in a liquidity pool, but it falls short in one key area: it cannot respond to changes in relative token value.

What does this mean? Well in the above example we used the equation of
y + 4x = 50, which means the constant m represents the token exchange rate between the two tokens (1 of X is worth 4 of Y).

However, the price of crypto assets are never constant, in fact token prices are known to be very volatile. So how will a change in price relative price of the tokens affect the pool?

Using the same equation of y + 4x = 50. Let’s assume that price of X rises sharply in all crypto markets relative to Y, and it’s now worth 5 of Y. Since m is a constant in our pricing model (value of 4), the curve cannot change the exchange rate between token X and Y. This will lead to a sharp increase in the demand of X since it is underpriced in our liquidity pool.

1.2.2 Emptying of the pool

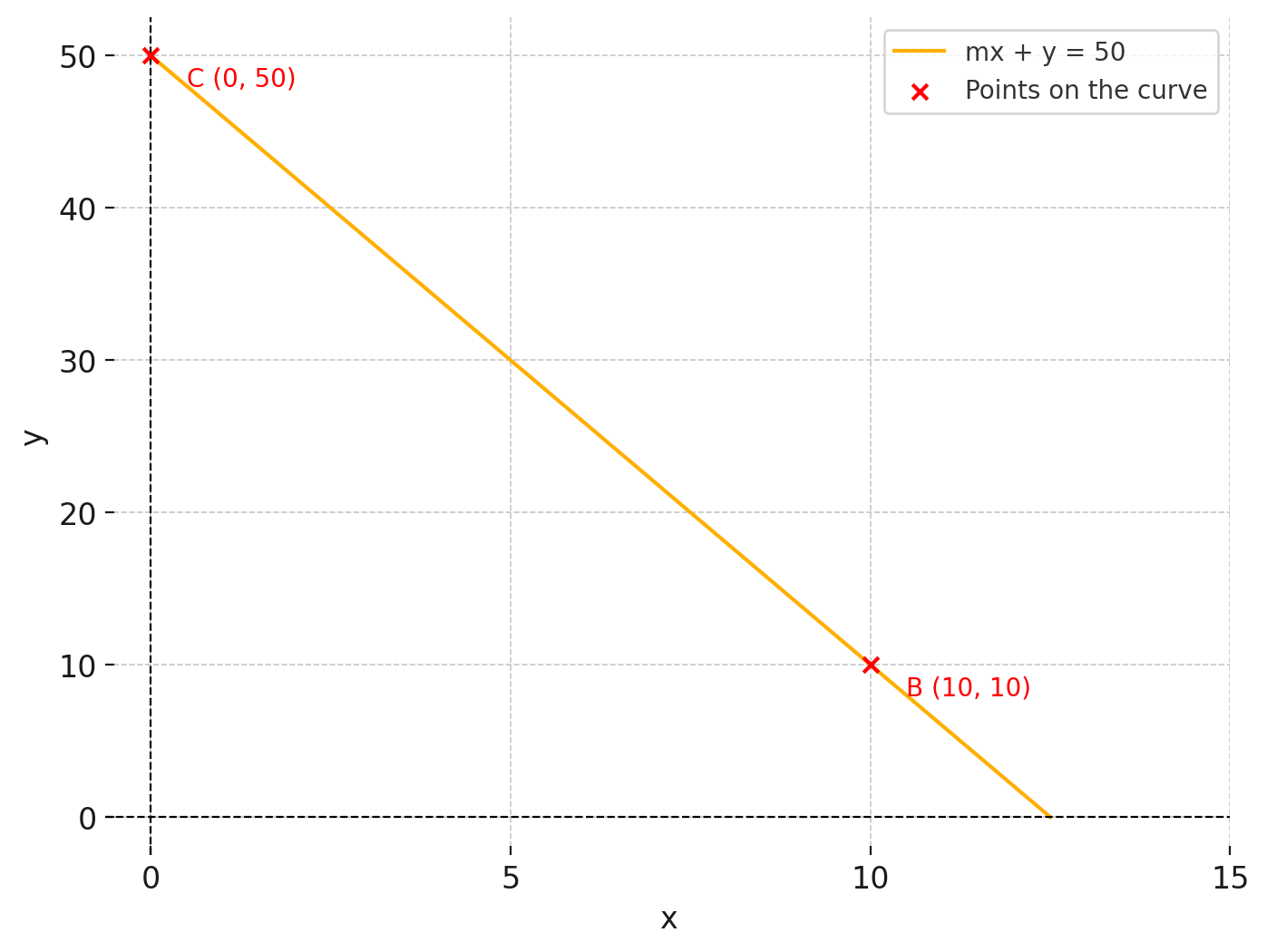Emptying of Token X from our liquidity pool

This sharp increase in demand is represented by the change from point B to point C, as traders flock to take advantage of the price discrepancy of X relative to Y in our pool (1 X to 4 Y) versus the open market (1 X to 5 Y). By buying each X for 4Y, traders can now sell it on the open market for 5Y to garner a profit.

Our liquidity pool is now rendered useless with a deviation of relative token price, which makes it a rather bad model for our liquidity pool. Can we find a model that can adapt to changing token prices?

1.3 Price Curve (Constant Product)

The constant product curve is an alternative to the constant sum curve in liquidity pools, and is represented with the mathematical expression where:

1. Coordinates X and Y represent the number of tokens in the pool at any point
2. Gradient Value at any point on the curve represents the exchange rate (at that particular point)
3. Constant K represents in total value in the pool

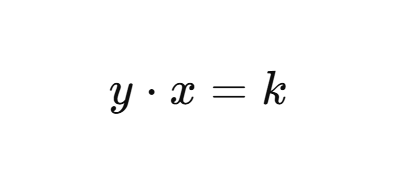Constant Product Equation

Again, let’s look at the equation as a graph:

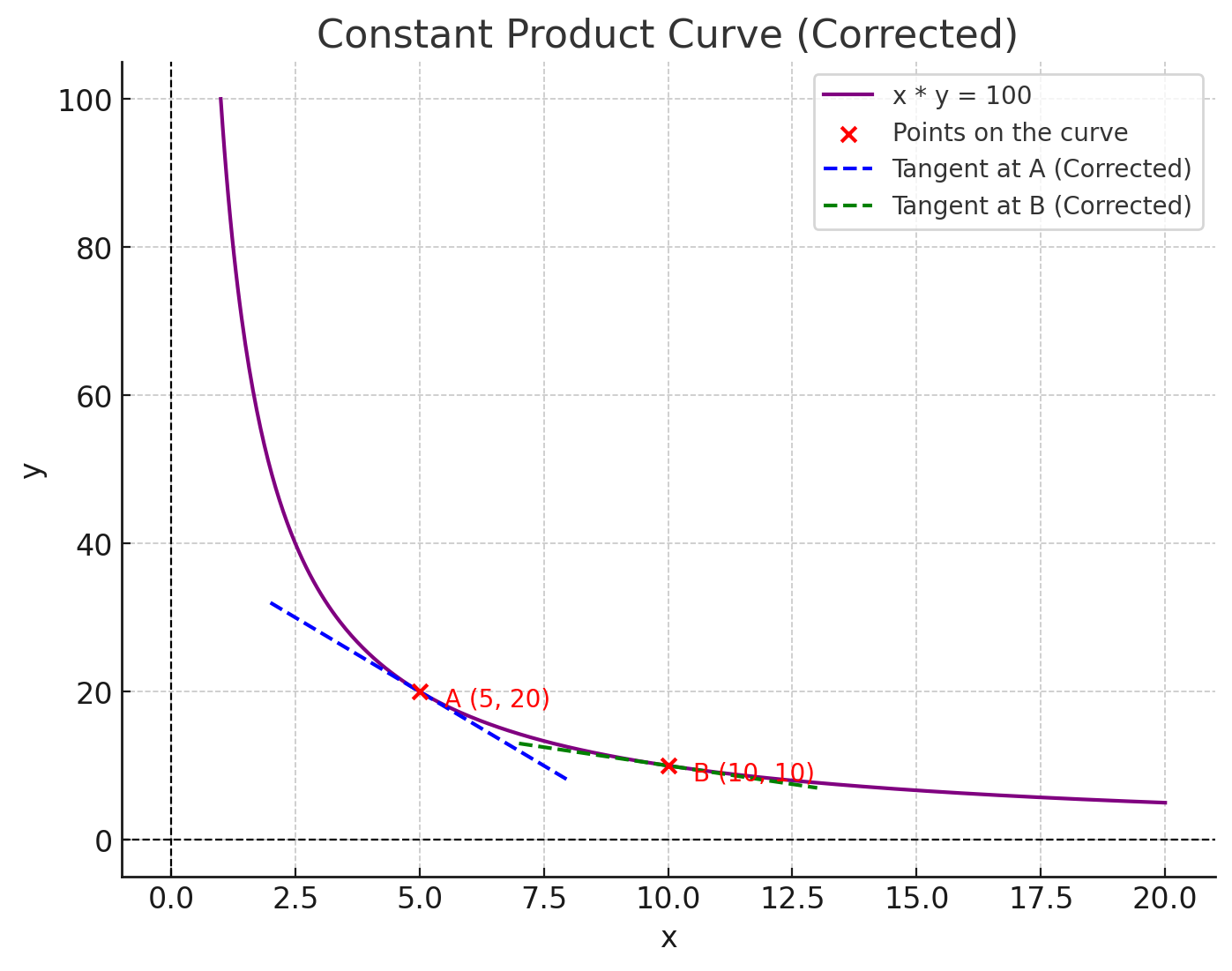Constant Product Graph

In this curve, the liquidity pool is represented with the equation y * x = 100, with the k value of 100.

In the above graph we have two coordinates A and B (5,20 and 15,6) that represent different state of the pools, where user’s interaction with the pool changes the coordinates along the line of the curve, changing the number of each token in the pool.

1.3.1 Price Adaptation

Remember how the main issue with constant sum pools is the inability to adapt to price changes in the open market? And the gradient at a particular point represents the price (exchange rate) of each token? Let’s look at how the product curve is able to adapt and change token prices as traders interact with the pool.

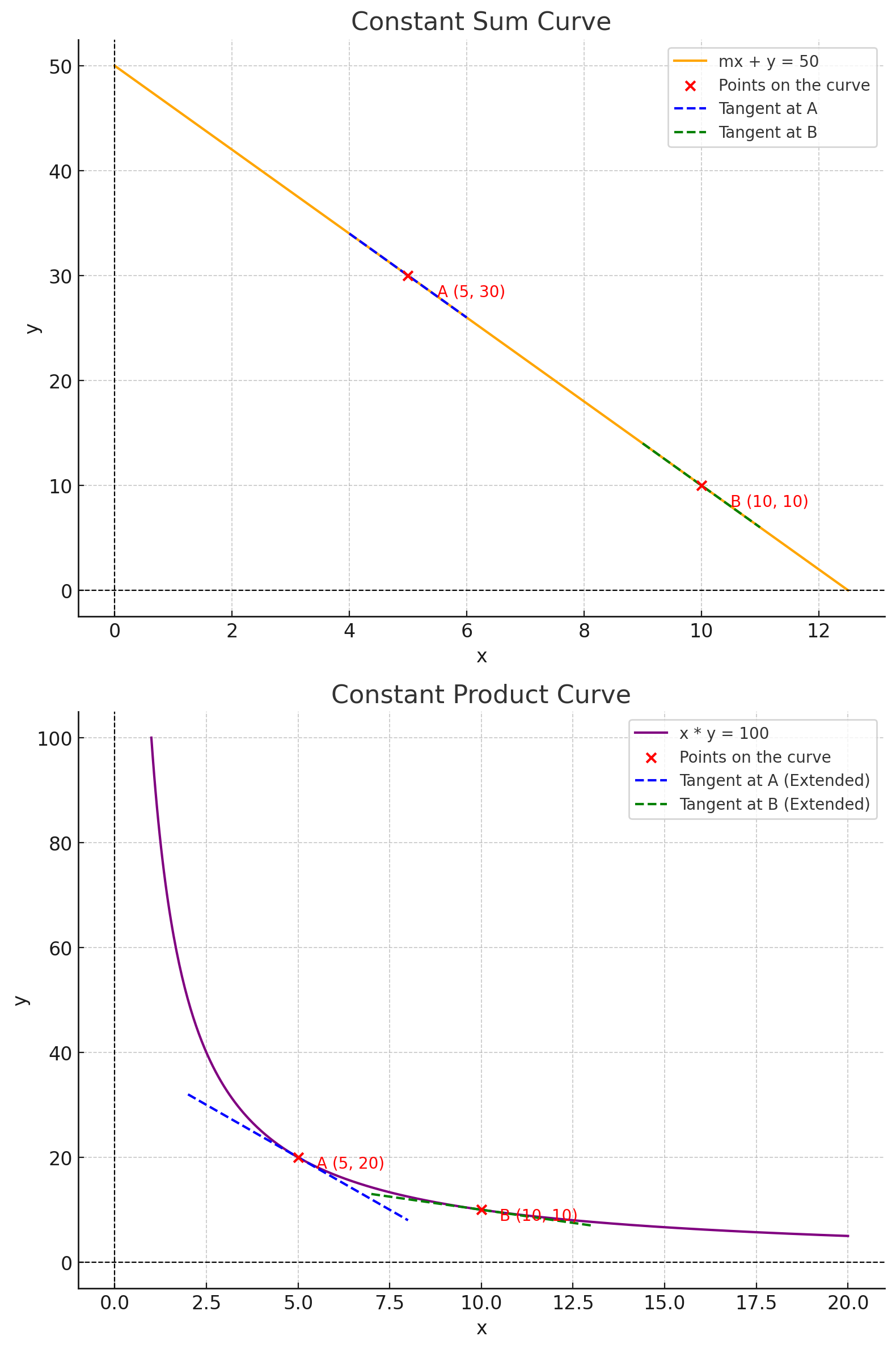Gradient/Exchange rate changes as token ratio changes

Notice a movement from point A to point B on the product curve yields a different gradient (see tangent lines) and hence a new exchange rate at the new coordinates at B, unlike the sum curve (the gradient is always constant).

As a user drains the pool of X, the price of X steadily becomes more expensive relative to Y. As traders exploit price differences between the liquidity pool and the exchange, the price of the tokens relative to each other adapts with each trade until the new price is reflective of the price of the tokens in the open market.

2. Slippage

Constant product are the most commonly used mechanism for liquidity pools, but it doesn’t come without its issues.

The price adaptation mechanism can still cause issues for the curve especially when liquidity is low. Without an adequate number of tokens in the pool, price fluctuations can be too extreme for traders to use the pool.

Depending on the size of the trade relative to the pool, traders can experience a difference between the expected price of the trade versus the actual price of the trade is being executed. This difference is called slippage

It’s a tad unintuitive to grasp, so let’s delve deeper to see how this works.

2.1 Slippage mechanism

We’ll be going back to the original product curve that we worked with earlier:

User trades the pool from Point B to Point A

Before the trade, let’s assume a pool state at coordinate B, with 10 of token Y and 10 of token X. By finding the gradient at that point, we realise that exchange rate between the tokens is 1:1. Let’s say a user wants to buy 5 of token X, he would expect to pay 5 of token Y.

However, this isn’t the case. To satisfy the product formula of x*y, the user actually has to pay 10 Y instead, as the pool requires a total token Y quantity of 20 at point A. Hence the user has to pay 10Y tokens. This difference in expected price of 5Y tokens is what we deemed as slippage

2.2 Lowering Slippage

Slippage is an inherent characteristic of trading with a product pool. But how do we reduce it? Well, you may have realised it, but the most important factor that determines the magnitude of slippage is the size of the trade relative to the size of the pool.

Look at this graph with 100 tokens of Y and 100 tokens of X:

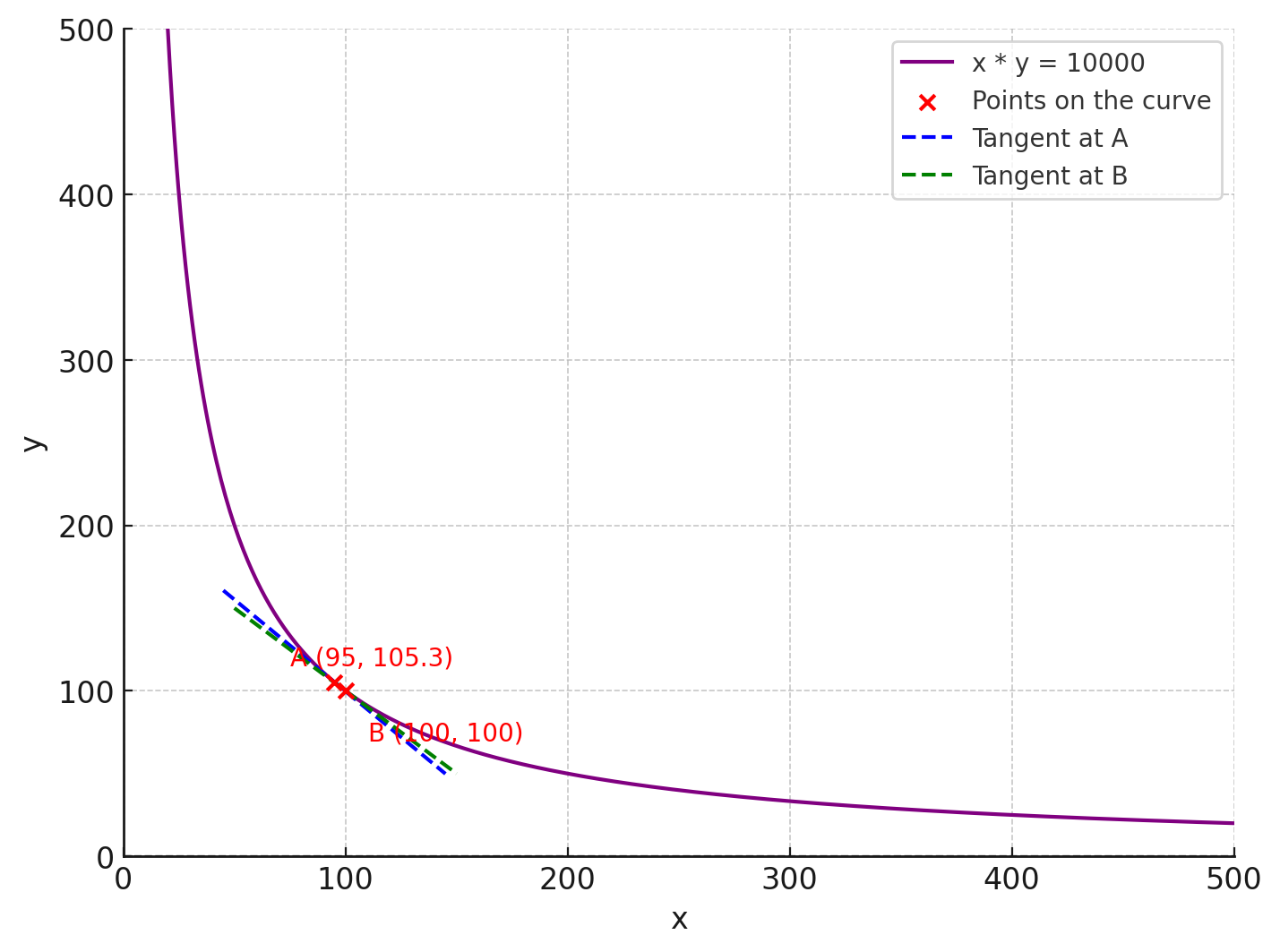Product Pool with much higher liquidity

Notice how the gradient (hence price) difference between each point is much smaller?

Now a user who wants to buy 5X, only must pay 5.3Y, as the pool needs a Y token quantity of 105.3 to satisfy the pool product of x*y=10000. The slippage of 0.3Y is much smaller compared to the slippage the previous pool.

Hence, slippage can easily be mediated with a high amount liquidity in the pool!

3. More liquidity

Now we know how important liquidity is for price stability, there is a problem that remains: how do I attract enough liquidity for my pool to remain stable? There are two main ways the pool does this:

1. Liquidity Incentives
2. Transaction Fees

But before we explore the solutions to this issue, we need to first understand the nature of the issue of attracting liquidity

3.1 Cold Start Issue

When a liquidity pool is newly created, there is initially no liquidity in the pool, making it unattractive for traders.

The cold start issue for liquidity providers and AMMs refers to the challenge of attracting initial liquidity when a new pool.

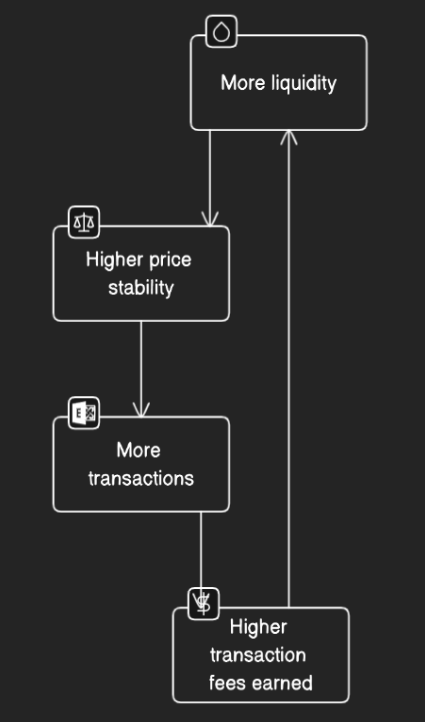Cyclical nature of attracting liquidity

Potential liquidity providers may be hesitant to provide liquidity to a new pool as there is no guarantee that there will be sufficient trading volume to earn transaction fees.

The pool needs high liquidity to be attract high trade volume, but it needs high trade volume to provide transaction fees to attract liquidity.

3.2 Liquidity Incentives

To overcome the cold start issue, AMMs and other DeFi protocols often use liquidity incentives to attract initial liquidity providers.

Liquidity incentives on ZilSwap

These incentives can take the form of additional rewards in tokens locked in the pool, which can be earned by the liquidity providers in addition to the regular transaction fees.

Governance tokens

Additionally, a new pool might offer a reward in its own governance token to traders who provide liquidity to a specific pool. These tokens give liquidity providers voting on proposals that influence pool protocols like adjusting of transaction fees and implementing new features

These rewards can make it more attractive for traders to provide liquidity, helping to overcome the cold start issue and kickstart trading activity in the AMM.

3.3 Transaction fees

Once the pool has enough liquidity to start attracting traders, the pool will charge smal transaction fees for traders (on top of the exchange rate), which will then distributed to liquidity providers.

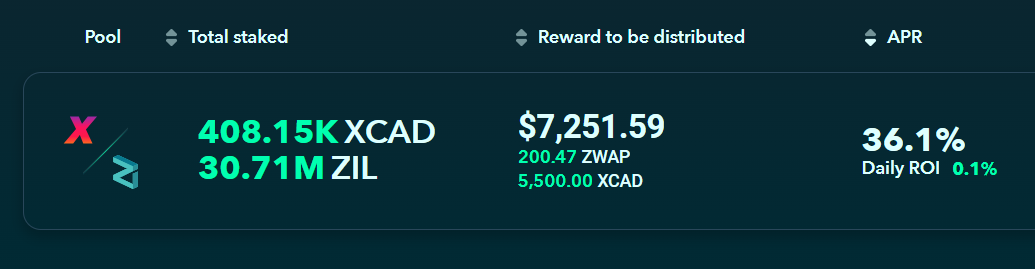Zilswap APR

Before providing liquidity for a pool, you can see how much you can earn by locking your tokens in pool, usually displayed as an annual percentage return (APR).

Note that an APR of 36% for example does not mean that the pool is charging 36% transaction fee for traders, usually new pools like you see from the above example have high liquidity incentives to attractive initial liquidity, which will be calculated into the APR.

Additionally, the APR of 36% calculated is not fixed, as APR is calculated based of transaction volume, which may or may not be stable. The net returns displayed is often a projection of how much volume the pool will have based off past trading volume.

4. Conclusion

The crux of decentralized finance, is its ability to replace traditional financial intermediaries (e.g., banks, brokers) with decentralized protocols to reduce costs and increase efficiency.

But the replacement of traditional financial services like money exchange, with its decentralized counterparts (automated market makers in this case), requires creativity and ingenuity in protocol design to be able to fulfill the same utility that it’s traditional equivalent.

In my view, I think liquidity pools and AMMs are a neat piece of engineering that leverages on incentives to create value for both traders and liquidity providers alike.